Cuando se empieza a bombear en un acuífero, cuya superficie freática inicial fuera horizontal; el agua comienza a fluir radialmente hacia el sondeo, y transcurrido un tiempo la superficie freática adquiere la forma de un cono, al que se lo denomina cono de depresión o abatimiento y éste genera un radio de influencia de pozo.
La principal aplicación planteada en este estudio es calcular la solución analítica para los radios de influencia de los pozos, a partir del cálculo del cono de abatimiento para los acuíferos confinados y no confinados, demostrando las soluciones propuestas por Theis y Neuman.
Primeramente se mencionan las características principales de un acuífero y se muestran las soluciones propuestas.
Características del Acuífero, mencionadas por Sanz P. y Méndez (2015):
Por su textura, la permeabilidad de los acuíferos puede ser debido a:
- Grietas y fisuras (kársticos)
- Porosidad intergranular (porosos de materiales detríticos)
- Conjunto de las dos anteriores.
Por su estructura pueden ser:
- Acuíferos libres o no confinados
- Acuíferos cautivos o confinados
- Acuíferos semiconfinados
El radio de influencia es más corto en los acuíferos porosos que en los kársticos y también más corto en los acuíferos libres que en los confinados. Por el contrario los conos de bombeos son más esbeltos (mayores descensos en el pozo) en los acuíferos libres y los acuíferos porosos.
Los tipos de ensayos de bombeo que se van a analizar en cada una de las clases de acuíferos se limitan al caso en que el caudal de bombeo es constante, bien en régimen variable o bien hasta conseguir un régimen permanente.
Se llama régimen permanente o estacionario cuando la distribución espacial del potencial es invariable con el tiempo. En general este régimen no se presenta en la realidad, pero resulta un concepto útil cuando se cumple de forma aproximada.
Cono de Abatimiento para Acuíferos Confinados
Fórmula de Theis
La primera expresión matemática que refleja la forma del cono de abatimiento en régimen variable se debe a Theis, que en 1935 la elaboró a partir de la similitud en el flujo del agua y el flujo de calor. La expresión es:
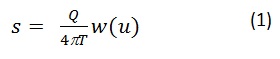
donde Q es el caudal, T es la transmisividad, W(u) es la función de pozo.
La integral en función de u que es el argumento de pozo:
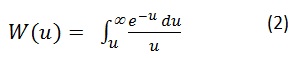
donde,

El argumento de pozo u, depende de r que es el radio, S es el coeficiente de almacenamiento, T es la transmisividad y t es el tiempo.
La integral puede expresarse en forma de serie (suma de infinitos sumandos), así:
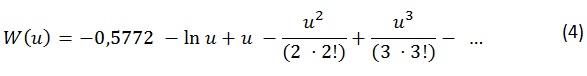
La solución de la integral para los distintos valores de u aparece tabulada en todos los textos de Hidrogeología. A continuación se incluye dicha tabla para el cálculo (Tabla 1).
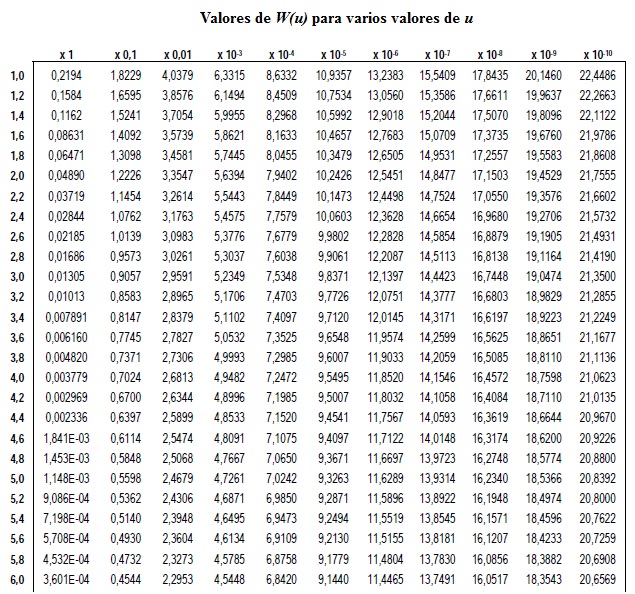
Tabla 1. Tabla normalizada para el cálculo de la función de pozo para acuíferos confinados.
Cono de Abatimiento para Acuíferos No Confinados
En el acuífero no confinado se distinguen tres fases en el bombeo:
- En la primera fase, al principio el descenso es rápido como si se tratara de un acuífero confinado.
- En la segunda fase, el descenso casi se estabiliza y desciende muy lentamente.
- En la tercera fase, el nivel de nuevo baja con el tiempo, pero no tan rápido como en la primera fase.
La primera y segunda fase siguen una ecuación similar a la de Theis, pero con diferentes valores para el coeficiente S:
- En la primera fase, S = coeficiente de almacenamiento por descompresión.
- En la tercera fase, S = porosidad eficaz (que es realmente el coeficiente de almacenamiento cuando se extrae agua por vaciado de poros).
Encontrar una solución analítica que refleje este proceso es más complejo que en acuíferos confinados (Theis).
Fórmula Neuman
Neuman (1972) enunció la siguiente ecuación, similar a la de confinados excepto por la función de pozo:
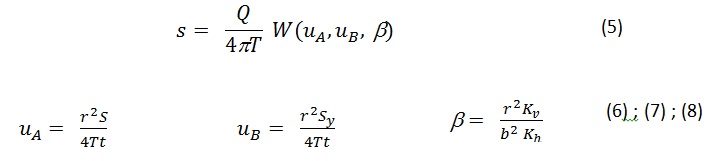
donde,
s = des censo a una distancia r transcurrido un tiempo t
Q = caudal de bombeo
T = transmisividad del acuífero
Kv = conductividad hidráulica vertical
Kh = conductividad hidráulica horizontal
S = coeficiente de almacenamiento elástico, por descompresión
Sy = porosidad eficaz (specific yield)
W = función tabulada en función de 1/uA y de 1/uB
La ec. (5) es la expresión conjunta de dos ecuaciones siguientes:
Para la primera fase de bombeo:
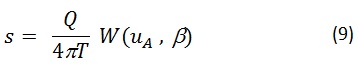
Para la primera fase de bombeo:
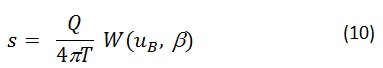
Resolución de las funciones se realiza con series o tablas normalizadas. A continuación se incluyen las tablas normalizadas para el cálculo (Tablas 2 y 3).
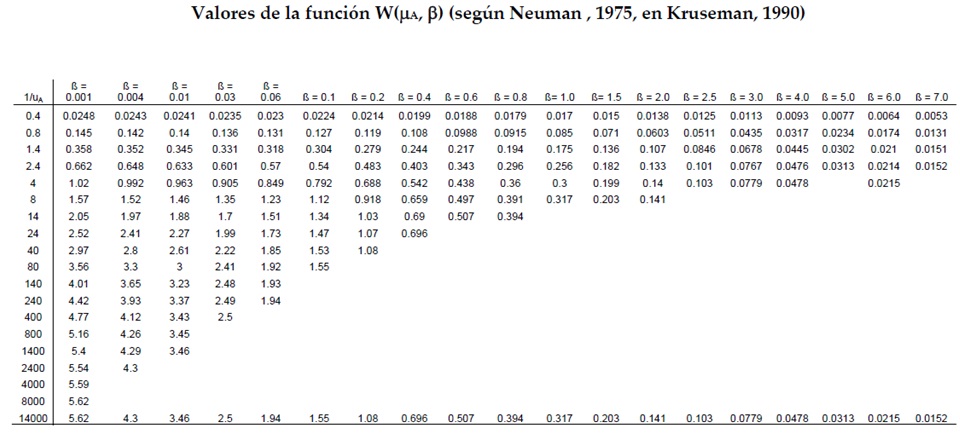
Tabla 2. Tabla normalizada para el cálculo de la función de pozo para acuíferos no confinados.
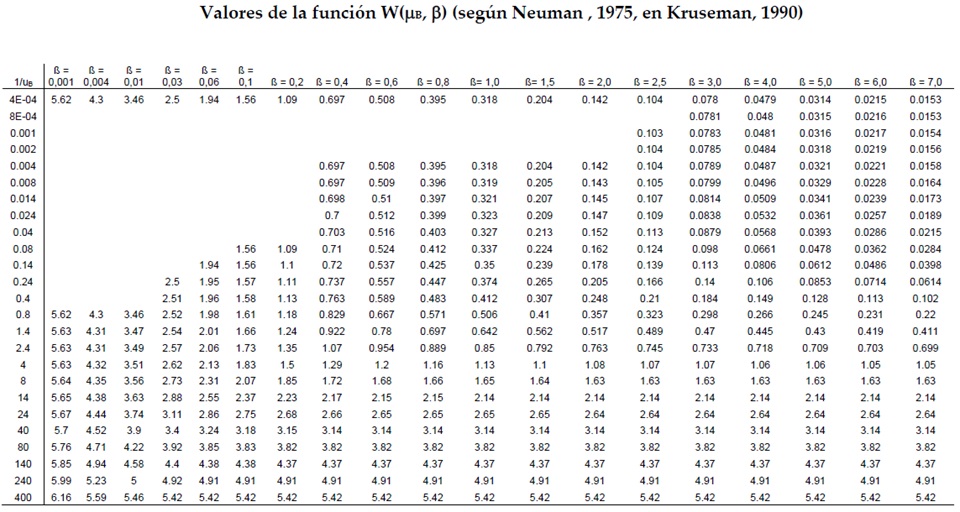
Tabla 3. Tabla normalizada para el cálculo de la función de pozo para acuíferos no confinados.
Referencias:
Freeze, R.A., and Cherry, J.A., 1979, Groundwater: Englewood Cliffs, NJ, Prentice-Hall, 604 p.
Sánchez San Román, J. F., 2012, Acuífero libres en régimen variable. Dpto. Geología. Universidad Salamanca – España. http://hidrologia.usal.es
Sánchez San Román, J. F., 2012, Hidráulica de captaciones: Fundamentos. Dpto. Geología. Universidad Salamanca – España. http://hidrologia.usal.es
Sanz-Pérez, E; Menéndez-Pidal, I., 2015, Hidráulica Subterránea. Ibergarceta Publicaciones, S.L., 2da Edición, 239 p.

muy bueno
Gracias, Rafael! Saludos.
Magnifico