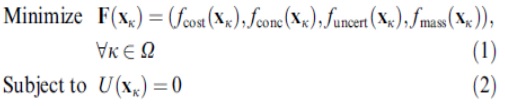Monthly Archives: julio 2017

Para proponer una red de pozos de monitoreo de calidad de agua subterránea, primeramente se realizó una revisión bibliográfica sobre los Algoritmos Multi-objetivos utilizados para el diseño de monitoreo de aguas subterráneas. En esta revisión fueron identificadas las características principales de cada artículo, presentadas en diferentes tablas de resumen (Tablas 1-4).

Todos los algoritmos utilizados en los artículos revisados se muestran en la Tabla 5, son resaltados los algoritmos con mejor rendimiento en cada uno.

Lista de artículos revisados:

1. Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design. Kollat, J. B., & Reed, P. M. (2005).
2. A computational scaling analysis of multiobjective evolutionary algorithms in long-term groundwater monitoring applications. Kollat, J. B., & Reed, P. M. (2007).
3. Save now, pay later? Multi-period many-objective groundwater monitoring design given systematic model errors and uncertainty. Reed, P. M., & Kollat, J. B. (2012).
4. How effective and efficient are multiobjective evolutionary algorithms at hydrologic model calibration? Tang, Y., Reed, P., & Wagener, T. (2005).

Tabla 1. Resumen del artículo: Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design [1].

Algoritmos Evolutivos Multiobjetivo (EMO) utilizados:	Algoritmo genético clasificado no dominado II (NSGAII). Algoritmo genético clasificado no dominado por Dominio de Epsilon II (e- NSGAII). Algoritmo Evolutivo Multiobjetivo por dominio de Epsilon (eMOEA). Algoritmo Evolutivo Pareto de Fuerza 2 (SPEA2).
Objetivos de los algoritmos:	Minimizar el costo de muestreo. Minimizar el error de estimación de la concentración de contaminantes. Minimizar la incertidumbre en la estimación de la concentración de contaminantes. Minimizar el error de estimación de la masa contaminante.
Evaluación y comparación:	3 métricas de rendimiento en tiempo de ejecución (convergencia, diversidad y epsilon-performance). 2 “unary metrics” (el indicador de hipervolumen y unary e-indicador). Función de logro empírico de primer orden.
Función objetivo general:	Mayores detalles en [1].
Escenario:	47 lugares de muestreo hipotéticos en una red de monitoreo de 25 pozos para conocer una instantánea en el tiempo durante ocho años luego de la liberación inicial del contaminante.
Objetivos de las métricas:	(i) alcanzar aproximaciones muy cercanas al óptimo frente pareto (es decir, convergencia), (ii) alcanzar soluciones a lo largo de toda la extensión del frente pareto (es decir, la diversidad) , (iii) maximizar la tasa de progreso de la búsqueda (la eficiencia computacional), y (iv) mostrar la menor sensibilidad a efectos de semilla aleatoria (confiabilidad de búsqueda).
Resultado:	Mejor rendimiento e-NSGAII.

 

Tabla 2. Resumen del artículo: A computational scaling analysis of multiobjective evolutionary algorithms in long-term groundwater monitoring applications [2].

Algoritmo Evolutivo Multiobjetivo (EMO) utilizado:	Algoritmo genético clasificado no dominado por Dominio de Epsilon II (e- NSGAII)
Objetivo del trabajo:	La complejidad computacional de usar el e-NSGAII para resolver una aplicación de LTM, mediante un análisis de escalación computacional. Utilizaron casos de prueba de tamaño variable de un total de 29 pozos para demostrar los efectos en relación al tamaño del problema (definidos como el número de pozos de monitoreo) en las necesidades computacionales al usar el E-NSGAII para aproximar el frente pareto con cuatro objetivos.
Objetivos de los algoritmos:	Minimizar el costo de muestreo. Minimizar el error de estimación de la concentración de contaminantes. Minimizar la incertidumbre en la estimación de la concentración de contaminantes. Minimizar el error de estimación de la masa contaminante.
Función objetivo general:	Mayores detalles en [2].
Escenario:	29 pozos
Resultado:	El conjunto de 18 a 25 casos de prueba de pozos reveló una relación lineal entre el tamaño del problema y el número de soluciones del frente pareto óptimo. La consideración de problemas más grandes requerirá que los usuarios acepten aproximaciones a sus conjuntos Pareto-óptimos.

 

Tabla 3. Resumen del artículo: Save now, pay later? Multi-period many-objective groundwater monitoring design given systematic model errors and uncertainty [3].

EMO utilizado:	Epsilon-Dominance Hierarchical Bayesian Optimization Algorithm (e-hBOA).
Objetivo del trabajo:	Estrategias Adaptativas para Muestreo en el Espacio y el Tiempo (ASSIST).
Objetivos del algoritmo:	Maximizar los ahorros de un plan de muestreo. Maximizar los valores de k de la matriz de ganancia K de Kalman. Minimizar el error en la muestra de contaminación en los lugares en donde se pronostica que existe contaminación a un nivel detectable. Maximizar la detección de los gradientes de flujo de masa pronosticados.
Función objetivo general:	Mayores detalles en [3].
Escenario:	21 pozos
Resultado:	Se demostró que el framework ASSIST es útil para entender la pluma dinámica y obtener estrategias de decisión en LTGM que evolucionan en el tiempo, así como el impacto espacio-temporal del muestreo desde ubicaciones específicas en el espacio y el tiempo.

 

Tabla 4. Resumen del artículo: How effective and efficient are multiobjective evolutionary algorithms at hydrologic model calibration? [4].

Algoritmos Evolutivos Multiobjetivo (EMO) utilizados:	Epsilon Dominance Nondominated Sorted Genetic Algorithm-II (e-NSGAII). Multiobjective Shuffled Complex EvolutionMetropolis algorithm (MOSCEM-UA). Strength Pareto Evolutionary Algorithm 2 (SPEA2).
Casos de prueba:	Test1: realizar la búsqueda global de manera eficaz, eficiente y confiable. Test2: calibrar la humedad del suelo para la cuenca de un río. Test3: aplicación de calibración del modelo hidrológico.
Evaluación y comparación:	Eficiencia, efectividad, fiabilidad y facilidad de uso de las herramientas EMO para la calibración de modelos hidrológicos.
Función objetivo:	–
Escenario:	–
Resultado:	Mejores rendimientos: Test1: SPEA2 Test2: e-NSGAII Test3: SPEA2 (pero e-NSGAII competitivo con SPEA2) En general, el rendimiento de MOSCEM-UA es alcanzado o superado por SPEA2 o e-NSGAII.

 

Tabla 5. Algoritmos utilizados en los artículos leídos – Tabla comparativa.

Artículo	NSGA II	e-NSGA II	eMOEA	SPEA2	e-hBOA	MOSCEM-UA
[1]	X	X	X	X	–	–
[2]	–	X	–	–	–	–
[3]	–	–	–	–	X	–
[4]	–	X	–	X	–	X

NSGAII: Algoritmo genético clasificado no dominado II.
e- NSGAII: Algoritmo genético clasificado no dominado por Dominio de Epsilon II.
eMOEA: Algoritmo Evolutivo Multiobjetivo por dominio de Epsilon
SPEA2: Algoritmo Evolutivo Pareto de Fuerza 2.
e-hBOA: Epsilon-Dominance Hierarchical Bayesian Optimization Algorithm.
MOSCEM-UA: Multiobjective Shuffled Complex EvolutionMetropolis algorithm.

Referencias:

[1] Kollat, J. B., & Reed, P. M. (2006). Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design. Advances in Water Resources, 29(6), 792-807.

[2] Kollat, J. B., & Reed, P. M. (2007). A computational scaling analysis of multiobjective evolutionary algorithms in long-term groundwater monitoring applications. Advances in Water Resources, 30(3), 408-419.

[3] Reed, P. M., & Kollat, J. B. (2012). Save now, pay later? Multi-period many-objective groundwater monitoring design given systematic model errors and uncertainty. Advances in Water Resources, 35, 55-68.

[4] Tang, Y., Reed, P., & Wagener, T. (2005). How effective and efficient are multiobjective evolutionary algorithms at hydrologic model calibration?. Hydrology and Earth System Sciences Discussions, 2(6), 2465-2520.